Guided Math In Action Book Study - Chapter 7

Chapter 7 of Guided Math in Action looks at the opportunities teachers have to build mathematical proficiency while having small groups. The chapter is broken down into five sections. These include:

• Conceptual understanding
• Procedural fluency
• Strategic competence
• Adaptive reasoning
• Mathematical disposition

Let's examine each one briefly.

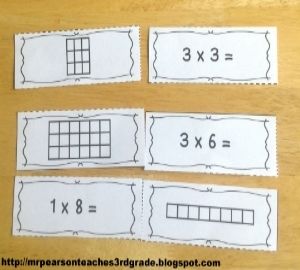
Conceptual Understanding. Conceptual understanding is when students know what they are doing on a conceptual level. This is often what we teach in our small groups. Dr. Newton give the example of using coins to help teach dividing decimals. There is also a sample lesson that shows how one teacher used this strategy, giving students 28 pennies and asking them to put the pennies into 4 groups. This portion is where manipulatives and the teacher toolkit comes into play.

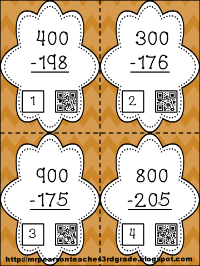
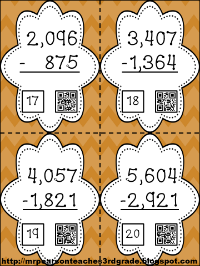
Procedural Fluency. Procedural fluency is knowing how to do mathematical procedures. It is when the students know how to do math. The example that is given in the text is adding numbers with 8 (a concept that I am totally going to "steal"). Students know the procedure of adding 2 to a number that ends in 8 to help make the number friendlier.

Strategic Competence. Strategic competence is when students are able to solve a problem and then explain their thinking as to how they were able to solve that problem. Students don't just jump straight for the answer, but they can show someone what they did to solve that particular problem. This can include using number lines, grids, or arrays. It is important for students to have a number of different ways to solve a problem.

Adaptive Reasoning. Adaptive reasoning is when students can think logically about math and then explain and justify why they chose that specific course of action. These mathematical discussions should allow the students to talk in an environment where they know their thoughts have value and they will not be made fun of because of the way they did a problem.

Mathematical Disposition. This area focuses on what students believe about math. How many students do you have that believe they are bad at math? As teachers, we need to promote perseverance, so that students will understand that some problems just take longer to solve. This involves scaffolding and helping student to stick with a problem or concept. Reflection is also a big part of this area.

I am only going to focus on answering the second question today. In my math classroom, we focus a lot on problem-solving. One of the key aspects is what we call the "Wrap Up." The Wrap Up is a concluding question (based on the day's lesson) in which students are asked to explain their thinking about a particular question. They are given the opportunity to solve the problem using words, numbers, or pictures. At the beginning of the year, the vast majority of the students will write one or two words. As the year progresses and the students become more adept at answering and solving math problems, their thinking becomes more elaborate and I begin to see longer explanations and pictures to illustrate their thinking. Of course, this type of thinking requires a good deal of scaffolding. Many third grade students try to take the easy way out when it comes to math, so building their perseverance is a huge part of teaching.

Be sure to join us on Sunday for Chapter 8.

An InLinkz Link-up

Two for Tuesday - Great Place Value Activities 50% Off Until Friday

It's Tuesday, so that means it must be time for another...

Two for Tuesday

To celebrate the fact that it's Tuesday (and school is about to start for most of us...sad but true), I've put two of my place value activities on sale for 50% off until Friday, August 1! Just click on any of the pictures below to go to my Teachers Pay Teachers store to take advantage of these great offers.

Place Value Scavenger Hunt

The first activity I have listed is the Place Value Scavenger Hunt. My students loved Scavenger Hunts! This particular activity had 28 questions that were related to place value concepts. The students were asked to round numbers, compare numbers, and write the numbers in different formats (standard, written, and expanded form). Each of the cards has a unique QR code associated with it.

The Place Value Scavenger Hunt makes a great center. I prepare the cards on cardstock and laminate them for durability. Then I cut out the cards and hang them randomly around the classroom. The students use the included recording sheet to write their answers down. After completing the activity, the students would use the classroom iPad to scan the QR codes using an app installed on the iPad. The QR code would provide the students with the correct answer, making the activity self-checking. Of course, the Scavenger Hunt can be used without an iPad as well.

This product normally sells for $3.50, but you can purchase it through Friday for just $1.75.

Check Writing - A Place Value Activity

The second activity is Check Writing - A Place Value Number Writing Activity. This activity is designed to student to the real world concept of check writing. The students are given the option of choosing from 24 different task cards and they are also given a blank check. The students are to fill out the check with the information on the card.

This was one of my students' favorite activities during our place value unit. They felt so grown up writing checks to me, their parents, and to the principal. One student even asked if she could take her checks to the principal. Too bad the checks weren't real.

Check Writing normally sells for $3.00, but, until Friday, it is on sale for $1.50. Please don't miss out and definitely share this with your friends and fellow teachers.

These are great activities to start the school year with, especially if your first unit is place value. You can also visit my Teachers Pay Teachers store for other great math activities. You can also follow my store to get updates when new products are available.

Guided Math in Action Book Study - Chapter 6

Chapter 6 is all about how to plan a Guided Math lesson. It was relatively short, but there was some really good stuff inside. I especially enjoyed the "peek in" of a Guided Math lesson.

Dr. Newton provides a framework for guided math that is broken into 3 sections. These sections include the mini-lesson, student practice, and share time.

• Mini-Lesson In the mini-lesson, it is our job as teachers to hook the students into that day's learning. We do this by making some kind of connection. I like to make the connection by telling a story. My students love to hear stories about my life or when I was a student in college and I always do my best to tie the story back to the lesson. After the hook, it is time to demonstrate the material.
• Student Practice After the teacher demonstration, it is time for the students to practice the skill being taught. This is the part of the lesson where the teacher and the student interact and discuss what they are doing as they work through the lesson. This would be a time for using whiteboards or playing games.
• Share Time The final part of the lesson is the share time, where students are asked questions about what they did during their practice time. Students can be interviewed one at a time or they can be asked to retell the main points of the lesson. The share time is then concluded by reinforcing the concepts one more time to clarify any confusion the students may have. The math centers are then explained and that group of students is released to go work.

The key take-away from this chapter is the need to plan out the lessons. Guided math is not something that can be done by the seat of your pants. It takes careful planning to be effective

Question 1: I have never been one to use a Guided Math lesson plan. Because of the way I build my small groups, I tend to do many of the same things each time I meet with a group. The key thing is that I already include all of the aspects of a guided math lesson when I meet with my small groups. We begin by reviewing the material. I show the students a couple of examples. The students are then given the opportunity to practice the lessons. Finally, we discuss what was done. I would like to become more conscientious about doing a more formal plan.

Question 2: When teaching from the concrete to the pictorial to the abstract, I always start with manipulatives. This can include base-10 blocks or coins or even cards. The students need something to hold in their hands. After they are used to moving the objects around, I show them how to draw pictures. A good example of this is showing the students how to draw arrays for multiplication. I also show the students how to use large squares, lines, and dots when using base-10 numbers. I have a blog post that I really need to write on how I teach my students to solve multiplication problems. I've been trying to write it for months.

---

It's hard to believe that we are almost finished with this book. Be sure to leave a comment about how you plan your guided math lessons or ways that you move from concrete to pictorial. I would love to hear some new ideas.

An InLinkz Link-up

Teaching Multiplication With Arrays and a Freebie

I have a confession. I absolutely love teaching multiplication with arrays. I love to draw them and I love to see my students drawing them, especially when they are attempting to solve a fact that they have not memorized yet. One of the projects that I am excited to have my students work on this coming school year is a giant multiplication chart where each space on the chart is filled with an array. I'll post pictures if/when we get it finished.

I realize that arrays may not be the most time efficient way of solving multiplication facts, especially when you get to larger facts like 11x12 or 12x10, but I think they provide students enough support and scaffolding as they learn their "smaller" facts to provide the foundation for those "bigger" facts.

One of the games that I will often have my students play in math centers (regardless of the topic) is Matching. Some people call it Memory, but I think that term may be copyrighted, so I call it Matching. The way the game is played is to have all of the cards turned face down on the table or floor. Students take turns flipping over two cards at a time. If the two cards are a match, the student keeps the cards. If not, he has to turn them back over. The key to the game is to keep an eye on the cards that have been flipped so that when a player's turn comes up, he can flip over cards he already knows. The player that makes the most matches is the winner.

       

I created a small freebie of this game and I want you to have it. Obviously you can use it as a Matching Game, but there are many different uses for it. If you do use it as a Matching Game, I would recommend printing it on card stock, but you probably know that already. Just click on the image below and it will download the activity.

If you are looking for other multiplication activities, I have several available in my Teachers Pay Teachers store. To take a look, click on the images below and it will take you to the product for more information.

I hope that you enjoy the freebie and I would love to hear how it works for you. Please leave a comment below to let me know how it is working for you and your classroom. You can also follow my blog or follow me on Facebook for other updates.

Five For Friday - Five Things I am Thankful For

It's time once again for Five for Friday, hosted by Doodle Bugs Teaching.

This week, I think I am going to write about five things I am thankful for.

My beautiful family. If you recall from last week, my wife just had a baby. She is a beautiful little girl, a true answer to prayer. In addition to my daughter, my wife and I also have four boys and they are just as amazing as you can imagine. Yes, they can be a handful at times, but they are wonderful little boys and I couldn't ask for a better family. Right now, as I type this, I am sitting in the garage, watching them ride their bikes. I am beyond blessed. And, while I don't want you to leave my blog, here is a link to my wife's blog where she wrote about our daughter in a much more beautiful way.

My health insurance. If you turn on the news, you are probably aware that healthcare and health insurance are big news lately. I have no desire to make political statements here, but I do want to say that I am thankful for the health insurance that my family has. Right now, our daughter is dealing with jaundice. I know that's not a serious thing, but her levels have been slowly increasing each day. As a result, she has had to have daily blood tests at the hospital and has been wrapped in a blue light blanket almost every hour of the day (I'm not a doctor, so I don't know the name for all of these things). Anyway, without our health insurance, I can't imagine what the costs would be.

Our trip to Disney World. This is a strange one for me to be thankful for today, but hear me out. I love Disney. I love Disney World. My wife and I took our boys to Disney World in June 2013 and we had a blast. We rented a van and drove from West Virginia to Orlando. That was an adventure in itself. Right now, we are planning another trip in June 2015. Yes, I realize that it is a little less than a year away and that I have an entire school year to get through between now and then, but it is giving me something to look forward to. Having a goal (and a pretty heft one at that. Have you seen how much it costs to go to Disney recently?) is helping to push me into working harder and to be a little more frugal with our funds. My wife and I have a goal of paying off our credit card before the trip and my desire to get to Disney is causing me to work on that even more. If you are interested, I recently wrote a post on ways that I am saving for my Disney trip. It might help you start saving for a trip of your own.

Running. I have mentioned running in each of the three Five for Fridays that I have participated in so far. Today, I am thankful for running because I am able to do it without it hurting. Earlier this year, I developed a really, really nasty case of tendinitis in my lower left leg. It hurt to walk or even stand up sometimes. Do you know how difficult it is to be a third grade teacher and not be able to walk? I kept trying to run and had to wear fancy compression sleeves on my leg in order to help alleviate some of the pain. Fortunately, most of the pain is gone. I ran almost 4 miles today and don't feel any discomfort. It's a great feeling. Now, if I could just get a little faster and go a little farther.

My Teachers Pay Teachers store. I am incredibly thankful for my Teachers Pay Teachers store. Having this store has done two things for me. First, I think it has made me a better teacher. By creating materials for the store, I have really "upped my game" because I want to make certain that the materials I am posting of top quality. Everything that I make for my store is something that I use with my own students and I want them to have the very best. Second, the money that I have made has helped as we have been paying off our credit card and saving for different things as a family. I am incredibly humbled that there are teachers who spend their hard-earned money on products that I have made and trust me to make products for them to use in their classrooms. It has been and continues to be a wonderful experience.

---

So, another week is in the books. Hard to believe that a few more of these and we will be back in school. I hope you enjoyed reading about the things I am thankful for. I would love for you to share something you are thankful for as well. It reminds me of that song we used to sing in church. "Count your blessings, name them one by one..."

Guided Math in Action Book Study - Chapter 5

Our book study continues with Chapter 5: "Balanced Assessment - The Key to Grouping Students." This chapter was all about using different assessment to help group students for small group instruction. Dr. Newton discusses ways for pre-assessment, ongoing (or formative) assessment, and evaluative (or summative) assessment. This chapter was chock full of practical ideas, but there were some things that I was left wondering about. More on that in just a bit.

Now, on to the questions.

Question 1 - The way our math framework is set up at my school, we do a "pre-assessment" every day. In third grade, we call it the problem of the day. This consists of 3 questions. The first question is a question from the previous day's lesson. It helps us to determine who is still understanding the material from the day before. The second question covers the new material we are learning that day. The final question is of a cyclical nature and can be from any topic we have covered up to the point, usually place value, multiplication, or fractions. These questions help us to determine who will be working with us in which groups that day. This is a bit different from the way Dr. Newton describes her pre-assessment. I love many of the ideas that she shared, but the sad reality (at least in my context) is that I often cannot fit all of those pieces in.

For on-going assessments, I use many of the centers activities that the students complete, as well as the first section of the problem of the day. I also give several written quizzes throughout the unit. These activities are designed to help me understand how the students are progressing. Our county recently began adopting a collection of questions (for lack of a better term) that are collected online. This allows us to create quizzes and tests that can be taken online. However, adoption of this practice has been slow. I guess old habits (written tests) die hard.

The summative assessments tend to be your typical paper and pencil tests.

Throughout the year, usually three times, our entire school gives a test that helps us to determine where a student is according to a benchmark score. It is the same test each time and the students are expected to make growth on the test throughout the year. This test is not without weakness, but it does allow me to determine what students may be falling behind in particular areas. The two main weaknesses are that the test includes questions that are not covered by our learning standards and the test is timed. Some students just don't test well when under time pressure.

Question 2 - There were a number of great ideas in this chapter. First, I am going to have to find some time to make versions of the interview forms Dr. Newton has in the book. I am reading my copy of the book on my iPad, so the formatting is a bit different.

Second, I need to find out what Math Running Records are. If you know, can you please leave a comment and direct me to the right place.

Finally, I am interested in putting together student portfolios. I will be working with special education students next year and this data will be necessary for IEP meetings. As I mentioned before, Evernote will be perfect for working on this. There is a feature on the app that allows Post-It notes to be photographed and cataloged. Perfect for anecdotal records and portfolios.

---

This brings us to the end of another chapter. If you haven't heard, there is a Q&A with Dr. Newton happening at Guided Math Adventures. Head over there for all the details. Thanks for participating.

An InLinkz Link-up

Two for Tuesday - Save 50% Through Friday

Today, I'm going to do something different. I'm going to offer two of my best-selling products from my Teachers Pay Teachers store at 50% of the regular price. I don't usually sell my products here on my blog (at least not this blatantly), so that's why it is different. So, I am linking up with the wonderful ladies of The Teaching Tribune for Two for Tuesday.

Subtraction Across Zeroes Task Cards

The first product is a set of task cards to help students practice subtracting across zeroes. A number of my students had difficulty with this particular topic, so I wanted to make something for them so that they could have extra practice during centers. It turned out that this product struck a nerve with others and it has sold more than any other product in my store. I recently updated the product and added several other items to it. Subtraction Across Zeroes sells for $4.00, but through Friday, July 25, it is on sale for 50%.

Identifying Fractions on a Number Line

The other product that is on sale is Identifying Fractions on a Number Line. To be honest, I was pleasantly surprised that this activity has been so popular. This is a set of 32 task cards that ask students to identify a fraction based on where the X is on the number line. It can be challenging because students have to determine how many sections the line has been divided into (the denominator) and find the position of the X (the numerator). This set of cards (like all of my task cards) are perfect for play Scoot, scavenger hunts, math centers, or for use in small groups. Identifying Fractions on a Number Line is normally $3.00, but is marked down to $1.50 until Friday.

I know that most of us still have a couple of weeks before school starts, but it is never too early to start planning ahead, especially when you can get an awesome deal like this. Hurry, these special prices are only available until Friday, July 25. And, while you are looking for great deals, be sure to head over to The Teaching Tribune to see other great offers.

Guided Math in Action Book Study - Chapter 3

Follow my blog with Bloglovin

Today's post is supposed to be about Chapters 3 and 4 from Guided Math in Action by Dr. Nicki Newton (have I told you that you should probably own a copy of this book?) However, my family had a pretty dramatic event take place this week and I was only able to prepare my thoughts for Chapter 3.

What was the event you ask? Well, my wife gave birth to a little girl on Friday afternoon. Catherine "Kate" Alice Pearson is now a member of the family. Isn't she beautiful?

So, while my wife has been recovering the hospital and getting acquainted with our new little one and her eating and sleeping and pooping habits, I have been at home taking care of our other four children. My wife and I are the proud parents of 4 boys (ages 8, 6, 3, and 2). Needless to say, there has not been a lot of time for reading and writing over the past couple of days. With that in mind, I hope that you will allow me some leeway with this post.

---

Chapter 3 is all about setting up the Guided Math framework. Dr. Newton is big on Math Workshop, but, as I've said before, you can use whatever math framework works best in your particular context. Right from the start, Dr. Newton makes it abundantly clear that you have to start with the routines from the very beginning. Students thrive on routine. The sooner you can get your routine established, the easier it will be to have the students follow along.

Among the first things to establish are the rules, consequences, and rewards. Students need to know what is expected of them when they are working in math. We need to make sure that there are positive expectations for the students and that they are clearly posted so that there is no disagreement about what needs to be done. The consequences for breaking those rules must also be established and followed. Finally, the students need to know the rewards. The key that Dr. Newton pointed out was not to "bankrupt" the system. If the students earn the points, they need to know that those points aren't going to be lost.

The other key aspect of the chapter is to build a teacher's toolkit. A toolkit is supposed to be at your meeting area so that you are completely prepared when your groups come back to work. The toolkit should include folders that include examples of student work, materials for keeping anecdotal records on the students, papers, pencils, different supplies like scissors and glue, and manipulatives like cards, dice, and rubber bands.

Now to the questions:

Do you have a teacher's toolkit? At this point, I don't a specific "toolkit." Having read this, I am going to work on putting together the necessary items that would be included in a toolkit. My friend Sarah has a great post about what she includes in her toolkit. You may want to take a look at her post to get some more ideas about what to include in your own toolkit.

Do your students have toolkits? All of our materials are kept in a central location. I have a cubby cart that holds all of the number cards, dice, and math games that the students may need when working at centers. This cart also has the rulers and crayons, as well as extra pencils and glue sticks. I do need to figure out a better way to organize the pencils and the glue sticks because I honestly think my students were eating them. I have never gone through as many glue sticks as I did last year.

How do you establish routines/expectations? I make my expectations and routines known from the first day. My students are told the routines, they tell the routines to each other, and they repeat the routines back to me. After that we practice the routines and if they aren't done correctly (which they typically aren't), we do them again. It usually only takes a few times of doing it over for the students to get the idea of what is expected. Additionally, I also make signs to hang up so that the students will have a constant reminder of what they should be doing.

---

Well, that brings us to the end of another chapter. Please be sure to read the other blogs that are participating, especially since my post is missing Chapter 4. And, like most of have said, if you haven't gotten a copy of the book yet, you really should. Amazon.com has a pretty good price on it.

An InLinkz Link-up

A Very Special Five for Friday

It's been quite a week, so here's a very special Five for Friday (hosted by Doodle Bugs Teaching).

---

Running: In my post last week, I mentioned that I needed to be running more than I was. Well, I guess that was a bit of a motivator because I did quite a bit of running this week. I ran Saturday, Sunday, Monday, and Thursday. I was pretty proud of myself on Thursday because I was able to break the 3-mile hump and ran 3.55 miles. Granted there was some walking in there because I was doing intervals, but I was pretty happy. Now I just need to continue increasing the size of the intervals. In time, in time.

Making Bow Ties: I am a bow tie guy. I wear bow ties almost every day at school. It is part of my "look" and students actually get upset with me if I don't have one on. Last year I got tired of wearing the same bow ties all the time, but they were too expensive for me to buy news ones. As a result, I started learning to make my own. This week I started on a new batch of ties. I finished one, but as you can see from the other pictures, I still have quite a mess in my work area (read: my wife's dining room). (The internet in the hospital room where I am currently working is too slow to handle Photobucket, so there is no picture of the mess). Most of them turn out fairly good. I just wish I had confidence enough in my abilities to offer them for sale.

It is probably cheating to make numbers 3-5 our new baby girl, but this whole week has been about preparing for her arrival. Tuesday morning my wife woke up at 4 am with pretty severe contractions. They continued to be strong and regular (every 10 minutes) for next couple of hours. We got up and got dressed, called the daycare parents to let them know my wife would not be taking any kids that day, and got our boys ready to go to grandma's house. Then the contractions stopped. We went to Hobby Lobby to walk around to see if we could get things going again. Nothing. No more contractions.

My wife had a doctor's appointment on Wednesday and that is when we got the news that she was going to be induced on Friday morning. So, as you are reading this and I am typing this, my wife is laying in a hospital bed receiving the necessary medicines to encourage our little girl to come out and play. It's kind of a surreal feeling. I have four boys already and I don't remember there being so much anticipation as there is with this baby. Maybe it's because it's a girl. A girl. I'm about to be the daddy to a little girl. Holy cow.

So that's my week in a nutshell. There will most likely be pictures in the near future, so please come back if you are interested. (Shameless self-promotion alert). You can follow me on Instagram at http://instagram.com/johnnyp5379 or on Facebook at http://facebook.com/mrpearsonteaches3rdgrade to see pictures there as well.

How I Became a Teacher - My Journey to 3rd Grade

It was never my intention to become a teacher. I never had any grand aspirations of "shaping the world of tomorrow" or "trying to make a difference" or any of that type of thing. In fact, I didn't even go to college with the intent of studying education. I went to college to study to become a pastor.

I attended Pensacola Christian College to study Pastoral Ministries. This is a great school if you are interested in studying the Bible. It is, however, not a school for everyone, but that has nothing to do with this story. After a semester or so, I quickly realized that, even though I still wanted to be a pastor, Pastoral Ministries was not for me. I didn't "fit in" with that crowd and so I needed to change my major. So, I decided to study to be a lawyer. From one side of the spectrum to the other, right?

When I spoke to my academic advisor about the major change, she suggested that I consider pursue something like history or English instead of pre-law. The reason was that, if studying law didn't work out, I would have something else to fall back on. With this thought in mind, I decided to change my major to Elementary Education. This would allow me to study a wider variety of subjects (math, science, history, English) instead of just focusing on one main area. Plus, there was about a 99:1 ratio of females to males in the Elementary Education department. In many of my classes, I was the only guy. Unfortunately, many of them were friends with the girl I was dating at the time, so...moving on.

While I was studying and practice-teaching, I was still preparing and desiring to become a pastor, more specifically a youth pastor. Turns out I was pretty good at being a teacher. Obviously I was a little rough around the edges and not what my professors would call a "star pupil," but I did pretty well. I completed my student teaching, graduated, and moved back home. I was volunteering at my church as the lead youth worker and I got a job at Faith Christian School as a 4th grade teacher. That was my introduction to full time education. That first year was incredible. I had a wonderful class of students. It was a small school, so I had a small class and I team-taught with a wonderful teacher, doing what I do today: math and science. During this year, I also got engaged to the girl who is now my wife (we've been married for 10 years!).

After getting engaged, I realized that I needed to make a little bit (by a little, I actually mean a lot) more money, so I began looking into working for the public school system in my county. I had a few connections from a summer job I had had in the personnel department and that helped me to get an interview. I interviewed and that fall I began my career as an elementary school teacher. I have been in the county for ten years at this point.

My teaching career has had some ups and some downs. I was still interested in becoming a youth pastor and even served as one part-time for nearly a year. I honestly believed that I was going to leave education and become a youth pastor full-time. It would appear that God had other plans for me. I am no longer in that ministry and have found a deeper love for my job as a third grade teacher. Part of that comes from my work with Teachers Pay Teachers. It is always interesting how people end up doing what they do.

My journey to becoming a teacher began with a desire to become a pastor. Through several twists and turns, I cannot imagine doing anything other than being a teacher. I have been blessed with an awesome team and great students and the county I work for takes very good care of me. I am truly blessed.

How did you become a teacher? Leave a comment and share your story.

Guided Math in Action Book Study - Chapters 1 and 2

Welcome to the first installment of the Guided Math in Action book study. I hope that you have had an opportunity to read through Chapters 1 and 2. If not, please consider picking up a copy of your own (available at Amazon.com). I promise it is a book that you will refer to again and again.

In the first chapter, we are introduced to a class that is involved in a guided math lesson. The teacher and her students were involved in a mini-lesson on subtraction with regrouping. I learned about a really great idea for students who aren't able to grasp the idea of Base-10 blocks or numbers. The teacher gave the students bundles of sticks. Each bundle of sticks had 10 sticks. When a student needed to regroup, he "broke" apart the bundle and moved those individual sticks to the ones place. Brilliant! I'm ashamed to admit that I had never considered doing that, but now I have a project!

The teacher worked with the students on a few questions together, then allowed them time to work independently. The other students in the class were involved in independent or group activities. After the group time was finished, the teacher walked the classroom and took notes (this is a perfect opportunity to use Evernote!) on what the students were doing. At the end of the math period, the class joined back up to share what they were doing in math that day. It was very interesting to see inside another teacher's classroom.

Question 1: Stretching myself can be difficult at times. I went to a college that had a very distinct way of teaching a class. There was little in the way of differentiation. We were taught to teach to the middle...not exactly the best way of doing things. I am very, very comfortable doing whole class teaching, but guess what? Not every student can learn that way! I have to stretch myself and be willing to try new things to help my students learn. If this means I am doing small groups with whiteboards one time and one-on-one with modeling clay another time, that's what I need to be willing to do. And while it can be difficult to keep track of the educational needs of 20+ students (hello, Evernote!), I need to come up with a way to do it. You may notice that I keep mentioning Evernote. Evernote is an app that is perfect for this.

Question 2: Third graders are the kings and queens of giving up before they even attempt to do something. If I had a dollar for every student who came up to me with the phrase "I don't get it!" before he had even put his pencil to the paper. In my classroom, we have a poster that says, "We Don't Do Easy." My students know they are responsible to keep trying a problem and to use multiple strategies in their attempt to solve a problem. There is no greater reward from me than a Knuckle Bump when a student works through and solves a problem she was struggling to solve.

In Chapter 2, Dr. Newton discusses the importance of a numerate environment. Such an environment allows the students to "safely" discuss their thinking and to challenge the thinking of other students. We want our students to be able to explain what they are thinking and how they were able to solve the problem.

Dr. Newtown also makes a big push for math workshop. While this is not the method that I currently use, many of the elements of math workshop can be found in my math classroom as well. The elements include:

• Calendar time
• Problem of the Day
• Whole Class Mini-Lesson
• Guided Math Groups/Centers
• Journals

Like I said above, I don't currently do a math workshop, but many of these elements (Problem of the Day, Mini-Lesson, Guided Math Groups, Centers, and Journals) are things I incorporate daily.

Question 1: While I believe that I have a numerate environment, I realize that there is always room for improvement. To that end, I am working to develop more math-related "decorations" for my classroom. I have started an "Anchor Charts" board on Pinterest. I am also looking for more ways to incorporate math word study. As I continue to develop these things, I will be certain to share them with you.

As I said at the beginning, I hope that you have been able to read along and are learning as much as I am. Please be sure to join me again on Sunday for Chapters 3 and 4.

An InLinkz Link-up

Guided Math in Action Book Study Kick-Off

One of my goals this summer was to read several professional books in an attempts to improve my teaching. So far, I haven't finished the first one (Guided Math by Laney Sammons.) However, I have the great privilege to team up with some other great teachers to participate in a book study on Guided Math in Action by Dr. Nicki Newton.

So, starting today and going through August 6, we will be reading through each chapter of the book and sharing our thoughts on the material. I am also going to be sharing how I plan to utilize the information in my classroom. I hope that you will come back each week and join the discussion.

Here is the schedule of posts:

If you are interested in reading along, you can purchase the book from Amazon.com or get a copy on your Kindle. I also hope that you will leave comments and share your thoughts. This should be fun!

An InLinkz Link-up

Five For Friday - My First One!

This is my first go at participating in a "Five for Friday" from Doodle Bugs Teaching. Let's Go!

#1 - The Lion King at the Kennedy Center. For my wife's birthday, I got us tickets to the Lion King at the Kennedy Center. It was pretty exciting because my parents came to stay with our boys and we were going to have a night away in a hotel. The only hiccup in the night was that my wife is 9 months pregnant and she started having contractions...every 10 minutes! I spent more time worrying about her than I did paying attention to the show. Turned out to be a false alarm, so no baby yet. My wife loved the show and I got to wear a new bow tie, so it was a good time after all.

#2 - Coffee. For Christmas, my wife got me this pretty cool contraption. It is a Cafejo My French Press. The French press comes with a K-Cup adapter, so I put my own coffee in and enjoy a delicious cup of coffee. Sometimes I use actual K-Cups (Coconut Mocha K-Cups are my favorite), but most of the time I buy bags of coffee from Target and fix my own cups. Good stuff!

#3 - Written Form Matching Cards. In preparation for the upcoming school year, I have been working on some games and activities for my class and to make available for purchase in my Teachers Pay Teachers store. This time I not only made a set of games, I created a sampler of the cards so that folks can try them out first. I also made a fancy pin to share about in on Pinterest. I would love for you to check it out and download the sampler to see if it is something you can use in your classroom. The full set is also available in my store.

#4 - Our new baby girl. As I mentioned in #1, my wife is nine months pregnant. It took forever to get to this point and now it seems like it will never end. Monday was a day of a lot of potential excitement...and a lot of disappointment. My wife had a doctor's appointment and they sent us to the hospital for a non-stress test because of her blood pressure. My wife is the only person who is more relaxed in the hospital than anywhere else. So after getting my hopes up that the baby might be coming this week, nothing happened. So no baby this week.

#5 - Running. I love to run, but I have not done any running at all since school got out. Maybe the summer is making me lazy or the heat is just too hot. Whatever my excuse is, it is a pretty bad one. Hopefully I will get my butt in gear again soon because I'm starting to look a little doughy again.

---

So, there you go. That's what's up for this week. Maybe I'll do another one next week...and some big news to share about the new baby! You never know!

I would love to hear from you. Please leave comments below and, if you haven't done so already, please follow me on Pinterest and Facebook.